DAGgummit

Feedback loops, sigma-separation -- and returning to a world of value conflicts

Stare at a table public statistician Stephen Fienberg made for 16 years, and maybe you’ll learn something.

For one thing, his logic endures and generalizes: polygraph screening programs shouldn’t be implemented at the National Labs, because they would threaten security. The reason is that they’re mass screenings for low-prevalence problems. Applying the maxim of probability theory known as Bayes’ rule (like Fienberg writing for the National Academy of Sciences did in Table S-1, above) shows that this entire class of mathematically identically structured programs risks backfiring under common conditions of rarity, persistent uncertainty, and secondary screening harms. Due to the inescapable trade-off between accuracy and error in our imperfect universe with its mostly probabilistic cues (signals), such programs then create either too many false positives, or too many false negatives. Fienberg was right: there’s no escaping the universal laws of mathematics, and most people don’t grok that due to the common cognitive distortion of the base rate bias.

For another thing, though, Fienberg requires revision to account for the bigger causal picture: We don’t know if lie detection programs net harm or advance security, because the test component (detection) is just one of at least three potentially interacting causal mechanisms by which they could work. Avoidance (deterrence) and elicitation (the bogus pipeline) are the others. And, unlike lie detection, they can be both modeled in mathematical terms, and validated scientifically in the field.

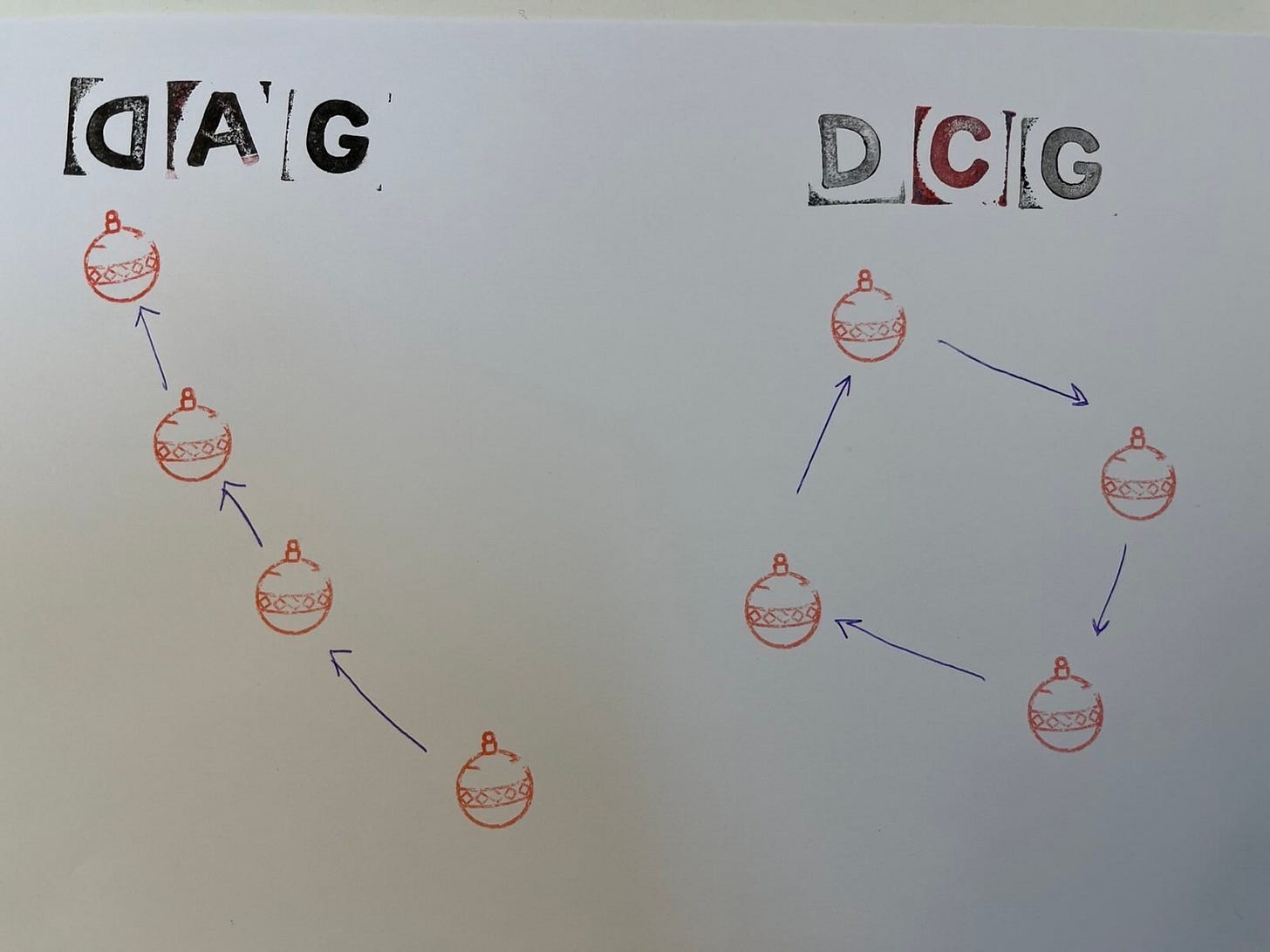
Let’s start with a directed acyclic graph (DAG)…

Deterrence takes a different type of graph

You might notice when you start to draw this that there’s just one problem: It doesn’t work (h/t Will Lowe). Deterrence is an equilibrium relation.

This is a fancy academic term for something most people already know: Strategic interactions involve layers of causality because we (well, most of us) have theory of mind. Bargaining in a market is also an equilibrium relation. So, famously, is sexual competition, as illustrated in the 2001 movie about mathematician John Nash (of the Nash equilibrium), “A Beautiful Mind.” So no, it’s not obscure, and yes, you need to know it — but that’s ok, because you sort-of already do.

Equilibria involve feedback loops, with causes and effects continually reinforcing one another. That breaks the “A” in DAG (for “acyclic”), because such loops are cyclic rather than one-way.

You can sort-of DAG the polygraph test mechanism by itself — no interrogation, no iteration. But what if its accuracy depends in part on the subject’s belief about how well the test works? That circular dependency means a DAG can’t represent the causal structure of even a one-off, test-mechanism-only polygraph.

(For a considerably prettier combination of these two pictures, see Figure 1 in Ragib Ahsan, David Arbour, and Elena Zheleva’s “Relational Causal Models with Cycles: Representation and Reasoning,” Proceedings of Machine Learning Research, Vol. 140:1–18, 2022, 1st Conference on Causal Learning and Reasoning.)

There’s no feedback loop in the DAG here (above left), where we might imagine belief in the polygraph causing nervousness causing “lie detection” causing the test outcome — as long as the subject’s belief doesn’t affect the test, and the outcome of the test doesn’t affect the belief. If it’s really a one-off, mechanical “lie detector,” and belief doesn’t affect the signal:noise ratio, then a DAG will do. But it has to be a one-way causal chain where the outcome can’t modify belief (e.g., “I failed the test but was telling the truth, so the test can’t be right”), and belief can’t modify outcome (e.g., “subject was visibly nervous, resulting in heightened skin conductance, so the baseline made the control question reaction lower”).

By contrast, if we think “lie detection” could also be partly about subject belief, even excluding the possibility of an interrogation component, then we need a DCG (directed cyclic graph). In the DCG here (above right), we might imagine belief in polygraph affecting nervousness affecting lie detection affecting the test outcome affecting the nervousness... The fact that there’s feedback here implicates the need for a DCG.

This surprises me, and may surprise my fellow causal revolution newbies, because DAGs are increasingly widely used in epidemiology and health research. But much of health also involves self-reinforcing loops. So why do we tend to see DAGs instead of DCGs?

DAGgummit, isn’t that the wrong model?

One reason might be that feedback loops in health research can take place over long time spans — think of vaccines lowering future disease transmission rates over months and years. Epidemiologists may then model them as multiple time-point DAGs instead of DCGs. After all, time is linear; this diagramming method works just fine in this context. I’ve seen it work better when the simple fact that time is linear helps you know how things need to be sequenced. I wouldn’t want to give up that tremendous logical thinking assistance that may be a feature of DAGs versus DCGs, unless I absolutely had to.

But the feedback loops in equilibrium models are immediate, so you have to. Strategic behavior updates in real time. I see a look in my boyfriend’s eyes when I ask him to do the dishes, and know to not ask anymore. We need DCGs to capture causal interactions with faster loops.

This isn’t just about polygraphs, but rather about deterrence and other strategic interactions, equilibria, and feedback loops more generally. And shifting from DAGs to DCGs means learning about 𝜎-separation (sigma-separation), the analogue for d-separation…

Hey, baby - your separation or mine?

When you think DAGs, think d-separation; when you think DCGs, think 𝜎-separation. What?

The d in d-separation refers to dependence (see also “d-separation without tears”). Its opposite is d-connection. Combining graphs and probabilities to draw conditional independence produces the special type of causal logic drawing known as a DAG. d-separation determines conditional independence by blocking paths in an acyclic structure. Thus, it breaks down when the graph loops. And yet, not all hope is lost…

𝜎-separation is a generalization of d-separation that works in DCGs. It adjusts for equilibrium dependencies by accounting for the cyclic nature of causal influences given feedback. By identifying when information flow is blocked (regardless of whether the graph is cyclic or acyclic), 𝜎-separation works in both types of {graph + probability} constructs (DAGs and DCGs).

For example, imagine a polygrapher believes a subject is nervous because he’s lying. The subject, in turn, believes the examiner is already convinced of his guilt and reacts accordingly. The dynamic loops.

In a DAG, d-separation would signal that, once we observe nervousness, the relationship between belief and outcome should be blocked. In a DCG, 𝜎-separation recognizes that the outcome itself affects belief, which then affects nervousness, and so on. The logic of conditional independence must account for this cyclic dependency. That accounting lets us better model feedback loops in equilibria relations where outcomes and expectations co-evolve dynamically. Think strategic behavior, deterrence, and belief-driven physiological responses.

A number of people seem to be doing cutting-edge AI/ML research involving equilibria relations with graphs, although some of them appear to have been doing it for 30+ years. (More on this in a future post that I’m guessing needs to gloss work by Stephen Lauritzen, Clark Glymour / Richard Scheines / Peter Spirtes, and Bernhard Schölkopf. Suggestions welcome.)

A beautiful lie

The security community argument for polygraph screening and other “dumb” security screenings (including next-generation “lie detection” programs that share the polygraph’s pseudoscientific basis) has to do with the general equilibrium mechanism. Because these are strategic interactions, the argument goes, we can game people into better aggregate behavior — so we should. This mechanism is not nuts.

It’s especially persuasive when there’s a third causal mechanism in play anyway, the bogus pipeline. If believing you have a lie detector doesn’t just make people avoid the interaction or not do the crime (deterrence), but gets them to tell the truth about stuff they’d otherwise lie about (elicitation), then “lie detection” could help prevent serious crimes. If enough people believe it works, then maybe it works just enough to improve security. (The classic “security theater” as noble lie narrative.)

Maybe this can be worked out further like a Fermi problem or modeled, or maybe we don’t know. Either way, it probably breaks the model to talk about it. Oops.

For the time being, this looks like bad news for my joyous civil libertarian celebration that Bayes’ rule implies there is no conflict between security and liberty in programs of this structure. (That argument may or may not still be saved by an empirically-moored simulation of how different outcomes accrue to different values in contradiction of how people usually assume they do as a product of reification, as loosely described here.)

That we might actually have to grapple with irreducible value conflicts in politics should come as no surprise. But that we might net benefit as a society from precisely the types of programs Stephen Fienberg spent substantial time in his later years opposing is, to anyone familiar with his heart and mind of gold, an intriguing shock.

Contrary to Fienberg’s assessment, some dumb screening programs could be smart. As long as enough people are dumb enough to believe them. And enough people think my blog is boring.

Rest assured, gentle citizenry. My prose will ever remain longwinded and wonky for your protection!