Rethinking Risk
Count bodies, warn at-risk groups, and maybe then we can talk about informed consent
When you go to the doctor to discuss routine medical concerns — say, contraception, cancer screening, or depression — you get that handout. You know, the one showing the bodies. For contraception, it shows how risky different options are in terms of births and deaths. That lets a woman decide for herself how much she wants to prevent unintended pregnancy, even at the possible expense of dying from hormone-induced breast cancer or stroke. There’s a lot wrong with this approach in how much it simplifies complex empirical and ethical realities. But at least the woman gets to see a rough estimate of the bottom line — the possible life or death consequences of her choice — before she takes action.
Except not. This doesn’t happen. Not with contraception, cancer screening or treatment, psychiatric treatment, or any other number of common medical interventions. Informed consent doesn’t exist.
The significance of this absence is most obvious in medicine, where legal and ethical norms demand we do better. But the issue also goes far beyond medicine. Bad risk analysis limits how meaningful choice can be — for consumers, citizens, policy-makers, and others — in broad-ranging areas from border security to social services. Better risk analysis could help create informed consent and improve outcomes. That means better health, better policy, and a more just world. This post explains how.
The idea is simple, though the full example I work through is long: Risk communication should let people making life or death decisions know what they’re deciding. That means taking four steps:
Thinking about causes first, like metastasis —> cancer death.
Focusing on at-risk subgroups, like mothers when it comes to both contraception and breast cancer — since birth control failure and lethal breast cancer are much bigger risks for moms than for nulliparous (childless) women.
Highlighting outcomes that are likely to matter most, like croaking before your kids are grown.
Translating aggregate effect estimates of single options, like breast cancer risk from the pill, into comparative real-world risks for vulnerable subgroups in the final analysis. This applies the insight from John Gardner’s Grendel that “Alternatives exclude” — so we need to compare the outcomes of at least two real-world options, rather than just presenting the risks of one option in isolation, when we do risk communication. In the case of increased breast cancer risk from the pill versus withdrawal, highlighting these outcomes shows that death risks net out. The big difference is that hormonal contraception is far more effective; in trade for this increased efficacy, its associated increased breast cancer risk doesn’t seem to make it riskier in terms of mothers’ ultimate survival.
Doing all this is harder than it sounds, and the incentives are wrong for most scientists to bother doing it. I don’t contribute anything toward a solution to either of these problems. The empirical answer offered in this full example is incomplete and imperfect. It just improves on not trying to answer the net comparative survival question. The effort is also not original. I’m just reshuffling some well-known pieces to show how maybe people who want to do better public service science, can try. Rethinking risk seems like the road to developing the informed consent we think we have in medicine and policy, but that people (and ecosystems) are dying because we actually don’t.
That’s the big methods frame in which to think about this real-world example… If at any point you grow weary of my rabbit holing, just Ctrl + F “tl;dr” for the summary at the end.
Recap
As my rabid research methodology newsletter fans may remember, this is the long-awaited part 2 of my last post — which argued people are smart enough to use information to make better choices, but scientists are bad at giving them the information they need in a useable form. The immediate source of this consternation was Fitzpatrick et al’s recent article reporting increased breast cancer risk is associated with hormonal contraception, even when it doesn’t contain estrogen (“Combined and progestagen-only hormonal contraceptives and breast cancer risk: A UK nested case–control study and meta-analysis,” PLOS MEDICINE, March 21). One big problem with this totally normal, respectable analysis and the widespread discussion around it was that no one bothered estimating how many breast cancer deaths (not cases) might be associated with hormonal contraception, in comparison with how many pregnancy and birth-related deaths might be associated with failures from another contraceptive option women might choose instead. In other words, no one told women what many might consider the bottom line: How different contraceptive options net impact life or death.
“Show me the bodies!” I raved at my screen. Then I fell into my rabbit hole, doing and redoing the relevant calculations, only to be extracted for unrelated talks preparation and chocolate cake. Now I will proceed to show you the bodies, with a few caveats…
Subgroup Updating Is Hard
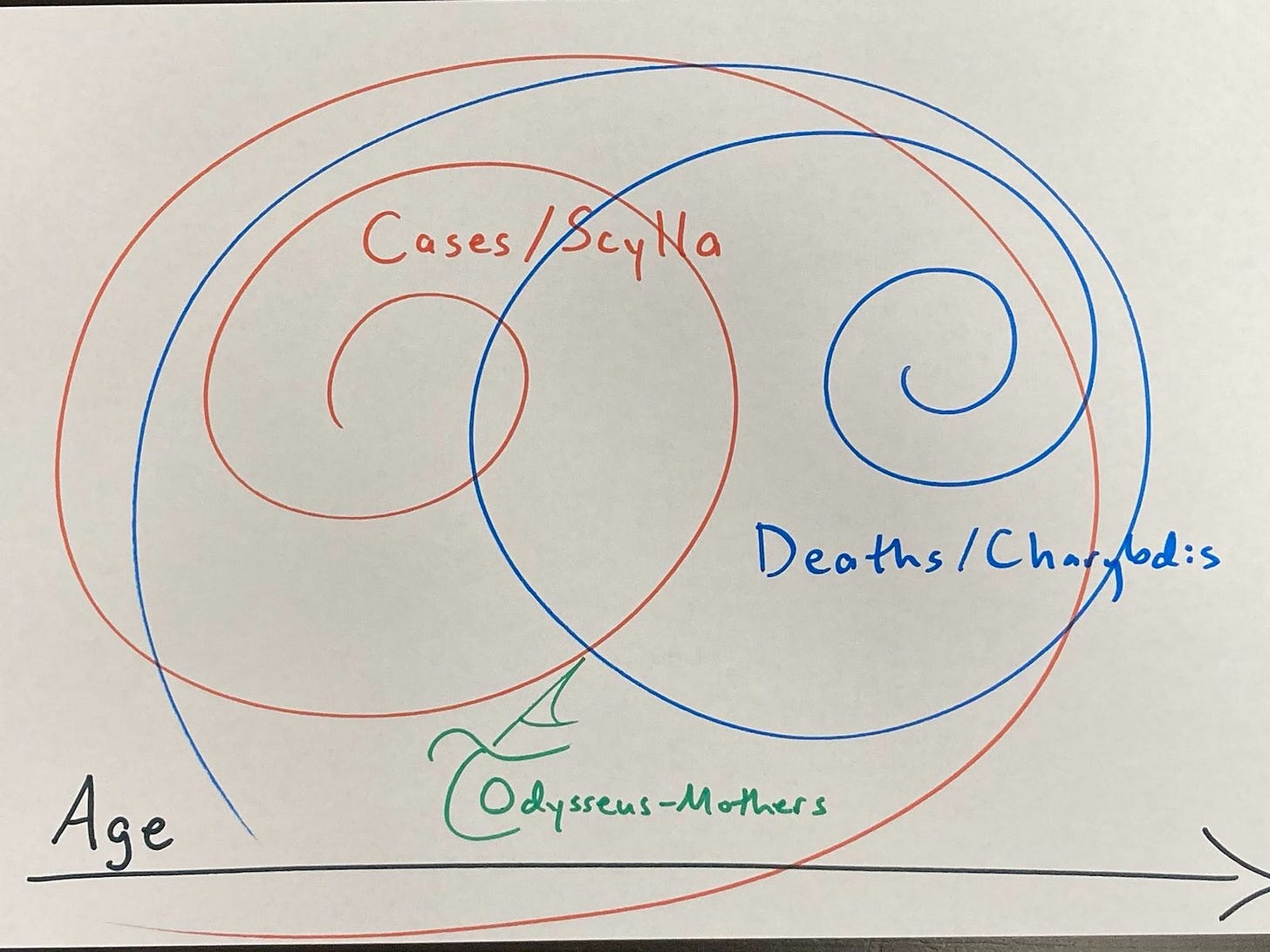
Honing in on the at-risk group of mothers to hash out survival numbers raised an interesting methodological wrinkle: What to do about opposing base rate trends that both impact deaths? Mothers face heightened risks of deadly breast cancer that rise with age at first birth — older first-time mothers risk more postpartum breast cancer cases. But younger mothers diagnosed with postpartum breast cancer suffer higher fatality likelihood by case. That looks like this:
More on this later. The main point is that this Scylla and Charybdis (opposing base rates) phenomenon complicates something as apparently simple as accounting for age with respect to postpartum breast cancer. For this and other empirical reasons, this example brackets age and hopes these opposing trends shake out. That could turn out to be a bad move, and I hope further research lets us find out either way.
What this phenomenon suggests to me is that, when I get excited about the potential of new(ish) methods and computing power to give us more meaningfully informed consent, it’s probably not that simple. That’s a nice segue to the next caveat: This may all be a pointless exercise in empowering people…
Consent Assumes Free Will
What if Sabine Hossenfelder is right that we don’t have free will? Informed consent discussions may then mainly represent a record of how different interests enact power — a sort of Seismic ripple of structure acting on agents who then believe themselves to be choosing, poor sods that we are. We can learn about this discourse as anthropologists, then, by analyzing the difference between what corrupt experts say in scientific and popular discourses — what I’ve sometimes called propaganda science — and what the evidence actually supports.
Sabine ties into the trauma and misinformation literatures (minute 17), pointing out that it’s hard to get something out of your brain once it is in there. Sing it, sister. This fits a deterministic universe — from particles to parliaments — in which none of this choice stuff is real. It’s turtles all the way down until you get to power, and then it was power all along. So there is no informed consent, because there is no free will. Joke’s on me and my calculations.
Nonetheless, acting as if free will exists might tend to generate different behavior within social systems (h/t Rafa). Maybe free will doesn’t exist, but ideology sure as hell does; perception can shape reality. In other words, maybe structure and previous experiences drive choices in deterministic ways that can yet be shaped and reshaped by narrative. That’s basically the promise of psychotherapy: Get your better present and future through a better past here. It’s also the power of propaganda and advertising, which seem to exert more reliable effects than therapy. And the hope of consciousness-raising, evangelizing, and other forms of positive future ideation.
None of that changes the likelihood that structure trumps agents, an assertion about which Robert Sapolsky also seems fairly confident. Just because you can dress power up with soft power, doesn’t mean it isn’t still power. Futility.
Speaking of structure trumping agents, let’s remember to reject the quaint fairy-tale of science as a logic-driven enterprise staffed by superhuman experts without bias who don’t respond to perverse incentives…
Something Is Rotten in the State of Science
Most risk communication doesn’t tell people what they need to know, in large part because most peer-reviewed science reports aggregate effect estimates instead of honing in on at-risk subgroups to whom we arguably owe heightened duties of care. Science does this because scientists’ perception of their job descriptions is shaped by norms, just like it is in other professions. Bad norms make bad science.
Structures shape these bad norms. For example, evil corporations pay good money, while doing better science in the public interest, generally, doesn’t pay. See, e.g., Andrew Gelman’s partial list of prominent statisticians who gunned for Big Tobacco on p. 45 (h/t Richard McElreath). This is power at work. It’s disgusting. There are crazy norms against calling this out for what it is, like we’re supposed to be polite about collateral murder if we want to be invited to dinner. Scientists can do better.
But ok, it’s not all black and white. Somehow, we are supposed to live in the structures of the world, finding a niche in the ecosystems of power and its contestations (which are also power), subsisting and reproducing (structures, goods, services, families)… And people do have to find a way to do that choosing from finite options, all of which may involve moral trade-offs, there being many principles to choose among prioritizing (Berlin’s value pluralism).
Still, science reformers generally agree that “publish or perish” incentives degrade and distort what should be (1) a lower volume of (2) higher quality science (3) more geared to serving the public interest. The proposal here, that we need to see comparative risk analyses pitting the possible life or death consequences of two realistic possible options (e.g., different common contraceptive methods), instead of looking at the risk of taking or not taking a particular one in a vacuum, pushes back against current norms shaped by these perverse incentives. It’s based on the idea that scientists need to think more about the ordinary people impacted by our research, and value people’s experiences and needs as knowledge. Again, we can do this; it just doesn’t pay.
So is all this talk of rethinking risk and reforming science (and science policy) hopeless? Where does it sit in some sort of practical context? What’s the political and social reality of science reform?
The Politics of Science Reform
I’m still new here, but it seems to me that science reform mostly addresses the perennial problems of stupidity and evil by working orthogonally to power. It tends to promote integrity, but not revolution; speaking truth to power, but not fighting it in activist or anti-authoritarian terms. Anti-authoritarian reformers tend to be summarily expelled even from halls of scientific power (e.g., Peter Gøtzsche and the Cochrane Collaborative). Observers tend to practice that liberal neutrality ideology that keeps people from getting things done (e.g., Retraction Watch doesn’t agitate for retractions). Nothing seems to have has changed in the attitude of modern Western publics toward people who tell inconvenient truths since Ibsen showed how people hated Dr. Stockmann for trying to protect them from contaminated spas.
So maybe science reform mostly works orthogonally to power, because it contests power, and that’s often unpopular. Working orthogonally to power can protect unpopular actors from retaliation. But that’s a fatal problem for science reform, if it’s a fatal problem for our species. Are the best minds of humanity’s last generation(s) fiddling with p-value reform while the Club of Rome burns? Is it wrong to stop (as I did) at methodological criticism and attempted popular translation of it, for example, when it comes to contesting industry-funded science claiming on the basis of insufficient evidence that antidepressants are safe in pregnancy?
You might say this sort of move merely reflects division of labor. I’m a research methodologist, so I do the nitty-gritty on a case study and then move onto the next rabbit hole; someone with different skills needs to run with the ball to get somewhere else with it. But this division is also about the structure of scientific institutions, or lack thereof. What if political science — science that speaks truth to power, with some bite backing up that bark — is a better idea than science that tries to stay out of the ring?
In theory, differently-structured scientific institutions could constrain and contest particularly egregious abuses of power. Methodologists have never clamored for the National Academy of Sciences to have a role in checking and balancing the government. What if they did?
On a smaller scale, it’s radical politics to envision informed consent in a world where it doesn’t exist. It would be nice if there were a whole national or international institute working to create it. Nominally, these things already exist in the form of various risk assessment organizations. But they tend to do bad science. See, e.g., the German Federal Institute for Risk Assessment’s exclusive breastfeeding promotion bullshit (and my critique thereof).
So maybe working orthogonally to power (like rogue methodologist ninjas) is the best way to do better science and science translation, as a matter of both political strategy and cognitive-emotional (and material?) necessity. Otherwise either you’re contesting power overtly, which means changing things and costing someone money, so people hate you, you don’t make money, and the isolation and precarity degrade your ability to do good work. Or else you’re in power instead of contesting it, and maybe structure selects for incompetence and corruption because corrupt interests promote themselves while excluding critics. Natural selection of bad science, as it were.
Caveats Recap
Subgroup updating is harder than it sounds. Informed consent assumes free will, which may not exist. Science has problems, and science reform works orthogonally to power, which seems problematic when bad science and science policy are literally killing people and planet — but maybe we can’t do any better. So possibly this is a threefold lost cause. With all those caveats, let’s go for…
THE LONG, HARD SLOG THROUGH THIS FULL EXAMPLE
Summary: Hormonal Contraception Net Prevents Births Without Increasing Deaths
Hormonal contraception is pretty safe, pregnancy and birth in wealthier settings are also pretty safe, and as a result, the death risks attributable to typical-use pill versus typical use withdrawal are roughly equivalent for mothers, an at-risk subgroup. Mothers are particularly vulnerable to breast cancer and death from it, as well as to contraceptive failure. So it’s worth zooming in on this subgroup, and letting them know that there’s no additional death risk associated with breast cancer from hormonal contraception (see Table 1). Only contraceptive benefit.
The death risks net out, because women face a double jeopardy of reproductive risk that men do not. Bearing children and preventing pregnancy can both kill. So calculating net deaths risks here requires counting both deaths from hormonal contraception-associated breast cancer, and deaths from pregnancy/birth when contraception fails.
These estimates simplify. For example, they ignore cardiovascular risks of estrogen-containing contraceptives that might shift the net death balance, particularly for at-risk women. Certain sub-sub-subgroups — like mothers over age 35 who smoke, or who have lupus or migraine with aura, and can’t tolerate progestin-only hormonal contraceptives (safer options in this context) — may have better survival chances with non-hormonal contraception. Then again, those groups, or subgroups within them, may also have heightened death risks from pregnancy/birth. For example, pregnant women with anti-phospholipid antibody syndrome may be more likely to die of VTE, and those with ITP may be more likely to die of hemorrhage, while also risking more from hormonal contraception with estrogen due to autoimmunity. Whereas women who have previously had certain pregnancy/birth complications (e.g., preeclampsia, thrombosis) are at heightened risk for having them again, and the calculus there may be clearer. Again, as with the opposite base rates phenomenon, more subgroup analyses for better informed consent sounds great. But doing them well is hard, and you have to draw the line somewhere.
These calculations correct denominator and decimal mistakes in the postpartum breast cancer literature, putting its incidence an order of magnitude lower than some other estimates (see Table 2). The analysis then compares birth and death risks of the pill versus withdrawal, bracketing the non-hormonal copper IUD. That bracketing is a big deal, since copper IUDs are highly effective, except in the immediate postpartum period (when expulsion risks are heightened), and don’t raise cancer risks. This pill-withdrawal comparison shows the incidence of postpartum breast cancer is two orders of magnitude smaller than that of pregnancy/birth; but it’s also two orders of magnitude deadlier (Table 3). That’s how the death risks net out: Hormonal contraception lowers pregnancy/birth risk (a lot) and raises breast cancer risk (a little), with the risk of death from metastatic postpartum breast cancer once it occurs being far greater than the risk of death from pregnancy/birth.
But we do know that hormonal contraception increases women’s breast cancer risk. A lot of people downplay this risk; “just get on the pill” is a thing. This is paternalistic crap. Patients need better information to make up their own minds. Giving it to them, though, is more complicated than it sounds. Even if all you care about is net survival, you still need to know how effective different contraceptive options are to figure that. The reason being that hypothetical projected deaths associated with hormonal contraception as compared with deaths associated with another option have to account for increased death risks from pregnancy/birth, or what’s usually meant by “maternal mortality.” So let’s work all this out piece by piece, starting with estimating contraceptive failure risks.
Contraceptive Failure Risks
Let’s say we’re comparing a best-case efficacy alternative birth control option with hormonal contraception, like the copper IUD (<1%) or perfect-use withdrawal (4%). The pregnancy prevention efficacy here is equal to or better than that of the pill under conditions of typical use, meaning hormonal contraception adds breast cancer risk for no net birth or death risk reduction. So why bother?
Because YMMV. A lot. For instance, IUD expulsion is frequent in the immediate postpartum period, perhaps especially for hormonal IUDs and in women who had vaginal births. Averbach et al estimated that risk at around 27.4% (95% CI 18.8–45.2), or 12.4% (4.8–43.1) for copper IUDs.
Similarly, typical-use withdrawal results in unintended pregnancies annually in around 20% of users. You might think both sets of figures are an order of magnitude larger than perfect-use hormonal contraception failure rates — but this is the real world, we’re looking at the subgroup of mothers, and birth control methods across the board appear less effective after you have kids. Congratulations, it’s a sibling.
The parity fertility effect — making babies, makes babies — is widely noted. And you can’t blame women for it (not that I can stop you) — because withdrawal is affected, too. See, e.g., Sundaram et al’s 2017 article “Contraceptive Failure in the United States: Estimates from the 2006–2010 National Survey of Family Growth,” Table 3, where parity swamps age category as a factor in contraceptive failure. Maybe having kids makes everybody tired. Maybe having a baby signals the body that it’s safe to have a baby and fertility increases because resource expenditure changes to favor it. Maybe uterine vascular developments during pregnancy increase implantation rates. We don’t know.
This effect bucks the conventional wisdom that female fertility goes off a cliff around age 35. But if you work in a women’s health-related field or have close female friends of a certain age, you probably know numerous women who had accidental pregnancies after having a baby, including after having had fertility problems or even IVF before. Having a baby boosts a woman’s fertility so much that some say it resets the fertility clock. Mainstream info sources like WebMD say that’s a myth, but Amy Kiefer at ExpectingScience.com nicely debunks those sources’ myth-debunking with evidence from studies suggesting that giving birth really does seem to help older women conceive again later. Whether they mean to, or not.
Limits and biases: Since parity seems to matter most, this analysis sticks with the subgroup of mothers. This approach may over-estimate birth risk and under-estimate death risk for older mothers. It also uses Sundaram et al’s data on failure rates for the pill and withdrawal — ditching their category “all hormonals and IUD” as unusable for this analysis, since hormonals other than the pill carry varying cancer risks, while the copper IUD carries no known cancer risk. In addition, this comparison overestimates birth risk associated with hormonal contraception, because other hormonal contraceptives (like hormonal IUDs) are generally more effective than the pill. It’s probably better to overestimate than underestimate this risk, since the idea is to tell at-risk people when to maybe duck. But it’s a bias nonetheless.
Comparative Birth and Death Risks of Common Contraception Methods in Mothers
The rest of this post proceeds as follows: First, Table 1 (below) shows estimated projected births and deaths in a hypothetical population of 100,000 UK mothers who wish to prevent pregnancy, and a brief discussion of what these numbers mean. Then, I list some possible ways to improve on these sorts of calculations. Next, the details of these calculations are spelled out in more detail than most people will care to read them. I highlight mistakes in postpartum breast cancer (PPBC) incidence estimates, which, when corrected, cause the deaths to net out. Lastly, there’s a quick summary of the whole thing bringing it back up to the general-interest level — where informed consent doesn’t really exist, but better science could help create it.
TABLE 1: Expected outcomes of common contraceptive methods in a hypothetical population of 100,000 mothers
This is a rough cut with problems. For instance, we don’t know if cancers associated with hormonal birth control really do act like postpartum breast cancers in terms of metastasis and death rates, when they occur in mothers or otherwise. We just know they would get counted as that subtype. More research is needed on the relationship between hormonal contraception and postpartum breast cancer subtypes and metastases/deaths.
It’s also worth noting the quantitative dimension here is flat. Life is multi-dimensional. Quality of life matters; hormonal birth control commonly causes nasty side effects like crippling depression. Quality of death matters, too; some women may prefer to risk dying (relatively quickly and privately) from pregnancy/birth, than (relatively slowly and publicly) from metastatic breast cancer associated with using hormones to prevent pregnancy. Others may prize something about living with fewer children, to run a small risk of dying for it. Or so abhor the thought of leaving orphans that whatever option promises fewer net deaths, wins.
In any event, actors like states and corporations are likely to have stronger preferences than the (fictive) collective of heterogeneous women about this. Big fish stakes — aggregated profits and demographic control — are considerable. So we have to be on guard against letting the powerful set the terms of the discourse on these existential life choices.
We Can Still Do Better
The main way I suspect this analysis could be improved is by showing more subgroup updating across all four cells applying Bayes’ Rule; that was the original idea, anyway. Mothers are a subgroup of women, and because they turn out to be especially at-risk for both birth control failure and breast cancer death, focusing on them seems appropriate. That focus need not be exclusive.
But it seems to me that we don’t have to crunch the numbers here to deduce the outcomes. Adding premenopausal women who don’t have children to these birth and death risk estimates would highlight that the survival benefit of running lower risks of pregnancy, birth, and PPBC by using more reliable birth control outweighs the death risk from hormonal contraception-caused breast cancer. The reason is that birth control appears to be more effective in nulliparous women (remember the parity fertility effect). So even fewer births means even lower death risks. In addition, giving birth spikes women’s breast cancer risk as well as their risk of death from breaset cancer; PPBC is a particularly lethal type of breast cancer. Breast cancers in nulliparous women are considerably less likely to metastasize and thus kill.
But less likely ain’t never, and this is aggregate logic with lots of wrinkles and uncertainties. What if Giersig is right and progestin-only contraception causes PPBC-like breast cancers even in nulliparous women? What if Stadel et al 1988 were right to flag nulliparous women who used oral contraceptives for more prolonged periods as being at particular risk for developing breast cancer before menopause? Some of the most apparently risk-averse women — nulliparous women on progestin-only contraceptives for a prolonged period — would then be making the riskiest gamble when it comes to preventing a decreasing number of pregnancies in trade for an increasing number of breast cancers as they age. But pregnancy/birth is also riskier for older women, and PPBC incidence is higher the older a woman is at her first birth. So we would need more subgroup data than I can find, including on progestin-only contraceptives and associated breast cancer cases, metastases, and deaths, to know better.
Here are some more possible next steps:
Thinking more about the timeframe (e.g., failure risks beyond the first year of contraceptive method use; longer-term hormonal contraception use and cancer risks).
Letting women tailor the risks according to their own preferred two contraceptive methods to compare, including whether they want to estimate failure rates under conditions of typical or perfect use. This matters because, as discussed, the specs can vary a lot. Different hormonal contraception methods have very different failure rates, from <1% for IUDs (with a big immediate postpartum asterisk), to up to 9% in typical use for the mini-pill. By comparison, withdrawal has around a 4% failure rate with perfect use, compared to around 10-20% with typical use. So how good your guy is at pulling out matters. A lot. A decent online calculator would let you account for that.
Better tailoring for age. It’s a truism that cancer risk rises with age, while fertility decreases with it So the older women get, the worse the net birth-to-death risk balance on hormonal contraception should become. This matters a lot clinically, in part because the older U.S. women get, the more likely they seem to be to be on birth control. So is something getting lost in clinical risk translation? Do younger women make some sort of rational if subconscious calculation to take more reproductive chances while the risks of pregnancy and childbirth are lower for both mother and child? Do older reproductive-age women make a similarly rational calculation to become more risk-averse over time due to learning, changing biology, different social expectations, or something else? What is going on here?
Better tailoring for parity. This analysis treated parity as binary, which was a useful way to make birth control failure rates more accurate within the subgroup of mothers. But parity isn’t binary. It has five possibly relevant facets: A standard approach would treat it as (1) a binary variable (birth, yes or no), (2) another binary variable (age at first birth, under or over 35), and (3) a continuous variable (time since birth). (4) Sometimes multiple births are factored in, but usually not. (5) Usually birth spacing isn’t factored in, but maybe it should be. My sense is that we can probably do better than this binary approach, but the how is complicated. Probably using Poisson regression, because PPBC deaths are rare enough events that we want to count them — like Park et al counted by annual breast cancer diagnosis incidence following first birth. Parity increases fertility, too, and treating it as binary in that context probably didn’t make a big difference. Where it may have mattered more was in calculating PPBC death risk, where things like age at first birth (over 35 being much riskier for PPBC), multiple births (possibly more risk), and birth spacing (less certain effects) may matter. Then again, the PPBC death incidence is so small that it may not be worth it to do this better.
More tailoring for at-risk groups. In the U.S., black women have a 40% higher breast cancer death rate compared to white women. Some black women (possibly of Western versus Eastern African ancestry) are at heightened risk for particularly lethal triple-negative breast cancer. Sundaram et al found black and Hispanic women were also at heightened risk for contraceptive failure compared to white women for the pill, condoms, and all methods combined, but not withdrawal. Moreover, U.S. black and Hispanic mothers have heightened maternal mortality and morbidity, an international phenomenon that extends to black women in the UK and elsewhere. So these are subgroups at heightened double jeopardy from both contraceptive failure and breast cancer. It seems worth estimating these risks, and the possible effect of hormonal contraception on triple-negative breast cancer in particular.
More causal diagramming, of which I have done some and show none because it’s hideously messy (DAGs on request). My contribution here is to hone in on deaths instead of cases as the outcome of interest, and highlight PPBC because of its relatively high metastasis and thus death rates, metastases being the primary cause of cancer deaths. But one of the larger causal problems in this story is that birth control → birth history → birth control (h/t Darren Dahley).
How do we as a society want to deal with the fact that different kinds of actors will tend to prioritize different outcomes here? Think individuals and couples who want families and survival, versus states and family planning NGOs pursuing population control policies, particularly in poorer contexts. This conflict of interests may drive hormonal contraceptive market growth. According to Fortune Business Insights, “Rising prevalence of unintended pregnancy and government participation to spread awareness about contraception are the key factors driving the market.” Hormonal contraception is a growing 17 billion dollar industry. Corporations profit as states and NGOs scale life-or-death payoffs to the population level. The big ethical concern with this is that I could be wrong about the net death balance, and then corporations and governments are killing poor women for profit and population control.
What about partner conflicts? Men’s socioeconomic and other forms of dominance over women often shapes reproductive decisions that are ultimately life or death — even though these decisions tend to impact women’s well-being, and sometimes their survival and existing children’s survival, more than they do men’s. Healthcare practitioners have a duty to not exacerbate these inequalities (“do no harm”). But discharging that duty is tough. Experts often pretend medical choices are individual choices, and much discourse frames pregnancy prevention and abortion as women’s rights. Reality is messier than that. It’s not clear this is a solveable problem. We can do better, though, than pretending that it’s all about individual choice and these tools only empower women. That’s not how power works.
What are some other ways to improve on this alternate way of using subgroup data? What about automating this sort of net risk comparison, making it faster and easier to make more complex and highly tailored versions? How hard would that be? Is difficulty (or impossibility) the reason we don’t already have an online calculator that lets patients tailor net risk comparison to make informed consent more meaningful like this? Or does this already exist and I missed it? It seems so basic and universally needed. But this one example was a lot of work, and doubtless just one little crank of the wheel better than not doing it out.
Down in the Weeds: Calculations
Births
Sundaram et al reported the pill has a 12-month probability of failure of 3.2% for women who’ve had no kids, versus 11.5% for mothers who’ve had one and 11.6% for mothers who’ve had 2+. Most mothers have more than one child — only 22% of U.S. mothers in 2014 ended their childbearing years with one child. So Table 1 calculated the pill failure rate as 11.6%, since the difference between 11.5 and 11.6 is minimal, 11.6 is more common, these are estimates, and erring on the side of slight overestimation is consistent with the goal of protecting at-risk subgroups.
For withdrawal, the parity differences look bigger: Sundaram et al again reported a substantial parity effect for withdrawal failure, this time with the 12-month probability of failure 8.4% for women who have had no children, 20.5% for mothers of one, and 27.7% for mothers of 2+. As previously noted, it seems common (including in scientific discourse) to blame women when birth control fails. But when having kids causes withdrawal failure rates to go up like this, it seems more logical to ask if maybe the dads were tired.
These numbers form the basis for the Table 1 births cell calculations. For withdrawal, that’s .205*22 (because of the 22% U.S. mothers with only one child) + .277 *78 (78% being the remainder of U.S. mothers) = x*100 = 26.116, or 26.1%. For the pill, that’s .116 * 10,000 = 1160, and for withdrawal, .261 * 10,000 = 2610. Then reducing assuming around 15% miscarriages (UK, US): .15*1160 = 174, and 1160-174 = 986, for a new pill failure birth estimate. And .15*2610=391.5, and 2610-391.5 = 2218.5, rounding up to 2219, for the withdrawal failure birth estimate.
But wait! Not all pregnancies end in birth or miscarriage. Some end in abortion. And, in this context, we don’t care. Here’s why…
The case for bracketing abortions
According to some estimates, most unintended pregnancies worldwide end in abortion (60%); Bearak et al 2020 say unintended pregnancies have recently declined while abortions of them as a proportion have increased. WEIRD countries look different, with much lower abortion rates. The Guttmacher Institute, a pro-choice NGO, says women abort a minority of unintended pregnancies in the UK (around 36%). Bearak et al 2021 (working for Guttmacher) model country-specific estimates of unintended pregnancy and abortion incidence, and estimate the U.S. rate as a little less (Figure 2). This remains a substantial minority of unintended pregnancies, even in very low-incidence abortion countries like the U.S. and UK. Very low-incidence means 17 abortions to 1000 reproductive-aged women, or 1.7%, the regional average abortion rate in Europe and Northern America per Bearak et al 2021.
It’s unclear how to account for this. Is that 36% of all unintended pregnancies, or of the miscarriage-reduced number? Most miscarriages occur earlier on, but so do most abortions; so accounting for that complexity somehow might make sense. A rough estimate might split the difference by averaging the reductions: (15% miscarriages + 36% abortions)/2 = 25.5% fewer UK births from unintended pregnancies. But then we also need to know what impact (if any) aborted pregnancy may have on possible postpartum breast cancer risk; pregnancy itself appears to increase risk, there’s been uncertainty and controversy around this question, and consensus abortion science is so bad that bracketing this whole issue seems mighty appealing. We may also want to think about whether people using withdrawal and people using the pill have different abortion rates when contraception fails. (Maybe not; Guttmacher says Catholics have more abortions than Protestants.)
Luckily, there are empirical and ethical grounds for bracketing abortion entirely — thus erring on the side of over-estimating births across the board. Empirically, figuring in abortions doesn’t make a huge difference, anyway. Using the 36% abortions figure and a post-miscarriages baseline number (overestimating abortions), births from pill failure are 986*.36=354.96, 986-354.96 = 631.04, or around 631 births, versus 2219*.36=798.84, 2219-798.84=1420.16, or around 1420 births from withdrawal failures, for a net birth risk of 2219-986=1233 in 10,000 (bracketing abortions) versus 1420-631= 789 (36% abortions). In other words, abortion doesn’t change net risk, because it figures in both rows.
Ethically, the first principle here is informed consent. Calculating in miscarriages while bracketing abortions to estimate births does that best. Miscarriages zero out the birth risk, whether you like it or not. Abortions do the same, but are a contingent medical intervention that may be unavailable or unacceptable to some women. So they don’t zero out maternal mortality when contraception fails.
The column name “unintended pregnancies” instead of “births” would avoid all this. But the point is to show life and death risks. Estimating births as a risk does that more concretely and accurately than estimating pregnancies, because all pregnancies are vulnerable to miscarriage, but not all pregnancies may be eligible (formally or informally) for abortion.
Absolute, relative, and net birth risks
According to these calculations, the absolute risk of birth is 2219/10,000= .2219 (around 22%) for withdrawal versus 986/10,000=.0986 (9.86%) for the pill.
The relative risk of birth is 2219/10,000 = x * 986/10,000, x = 2.25050, so withdrawal carries about a 2.25x increased risk of birth compared to the pill.
Net, withdrawal adds 2219-986=1233 births compared to the pill in a hypothetical population of 10,000 mothers. But that’s just net birth risk between the two contraception methods. We also want to see net death risk, and compare these payoffs.
Deaths
Estimating death risk from breast cancer is more complicated. Some complications can be named and bracketed, like heightened breast cancer risk for mothers who had their first baby later: PPBC risk is much higher for mothers who first gave birth aged 35+. The risk then continues to increase with advancing maternal age at first birth.
This group is growing as more women delay childbearing (UK, US). There’s much discussion (UK, US) about how this delay frequently results from structural conditions beyond women’s control. This “choice” often isn’t much of one, and sometimes it’s deadly. How deadly? What’s the incidence of PPBC?
Estimating this requires working through the research literature’s inconsistencies, unit and estimation method differences, and denominator and decimal mistakes. An example of inconsistencies: Park et al say in the last sentence of the first paragraph under their “Incidence Rate of Breast Cancer” heading that “The incidence rate of breast cancer in women with a first delivery between 2007 and 2012 was 8.84 per 10,000 person-years (95% CI 8.33-9.37) after 5 years and 21.06 (95% CI 19.87-22.31) per 10,000 person-years after 10 years.” This conflicts with their abstract estimating “The annual incidence rate of breast cancer after delivery increased every year (7.7 per 10,000 person-years after 5 years, 19.36 per 10,000 person-years after 10 years).” It also conflicts with their Table 2, which attributes a 19.32 (95% CI 16.33-22.86) per 10,000 person-years incidence rate to women in their 40s who had one, late baby; older first-time mothers are the represented group with the highest risk, yet the incidence rate point estimate here still doesn’t get up to that 21 per 10,000 person-years from under their “Incidence Rate of Breast Cancer” heading.
Such inconsistencies don’t matter for purposes of this post if there’s a consensus ballpark PPBC incidence estimate. And that 21/10,000 figure — or .0021, aka .21% — is roughly consistent with Nichols et al’s standard cumulative incidence estimate of 247 excess cases of breast cancer per 100,000 (.00247, or .247%) at age 50 comparing mothers with nulliparous women (non-mothers, p. 4). Person-time converts to rates: The rate is (# of new cases) / (total person-time at risk) (Alexander et al, no date). So it’s possible that ~.2% is both Park et al and Nichols et al’s incidence estimate — if they’re in comparable units. Are they?
Unit trouble
Nichols et al report “During 9.6 million person-years of follow-up, 18 826 incident cases of breast cancer were diagnosed.” Under Results, they say “During 9 625 727 person-years of follow-up (mean, 10.8 years [SD, 6.4])…” So their PPBC rate calculated from cases by person-years is 18,826/9,625,727 = .001955800325523. Park et al mention 10,000 person-years after 5 years and after 10 years, but don’t give total person-years, so it’s not possible to similarly cross-check their calculations on these units without doing a lot of calculations from their Table 1.
These units bother me. There may be nothing wrong with them; I may just be a little confused. But where do the units come from in the person-year-based rate calculation? If the rate is cases per total person-time at risk, then is Nichols et al’s .247% an average annual PPBC incidence for mothers for up to 34 years (the study’s follow-up period), and Park et al’s .21% an average annual incidence up to around 12 years? That may explain why Nichols et al’s is a little higher. Alternately, is ~.2% meant to be a cumulative rate for both of those (very different) time periods? It’s not entirely clear to me why dividing total new cases by total person-time at risk to make a rate would make the resulting rate annual, but maybe that makes sense to other people.
Given this unit trouble, it’s nice how Goddard et al 2019 put a clearer unit on their estimate: “Taking into account US annual statistics of 25 000 new breast cancer diagnoses in women 45 years or younger, just over 12 000 cases per year would meet the PPBC criterion for poor prognostic disease.” Now we’re counting annual cases instead of speaking in person-years. How does this compare to Park and Nichols’ estimates?
Denominator and decimal trouble
It’s not immediately clear, because the denominator is still missing. It should be mothers who gave birth in the preceding years, putting them at risk for PPBC for decades. The denominator is the at-risk group of all these mothers — roughly, mothers of minor children. But the temptation is to look for a count of women who gave birth in a particular year, and use that as a denominator. This mistake massively deflates the denominator — which in turn inflates the rate. That effect is apparent if you make the same mistake in calculating the incidence of spring among seasons: true incidence is one in four. Incorrectly calculating 1/2 would inflate the incidence and 1/8 would deflate it.
Current literature makes this mistake. Leading postpartum breast cancer researchers Virginia Borges, Traci Lyons, Doris Germain, and Pepper Schedin wrote in 2020:
Metrics related to reproductive history are not commonly included in breast cancer clinical datasets, such that the number of breast cancers that meet the definition of postpartum breast cancer (PPBC) is currently derived from best estimates. One approach to estimate global burden of PPBC is to utilize data obtained from developed countries, which show that approximately 13% of all breast cancers are young women with breast cancer (27, 28) and that approximately 50% of these cases have likely completed a pregnancy within 10 years of their diagnosis (29). This approach results in a global estimation of approximately 130,000 PPBC cases per year. An alternative approach is to determine the incidence of PPBC cases per completed pregnancy (again relying on data from developed countries) and then determining global burden based on number of pregnancies worldwide. Best estimates for PPBC cases in the United States for 2015 were approximately 13,000. On the basis of 4.5 million U.S. pregnancies/year, this would predict a PPBC incidence of 0.0028% (one in every ∼350 pregnancies). With approximately 130,000,000 live births globally per year, this estimation approach predicts 364,200 cases of PPBC worldwide (https://www.un.org/en/development/desa/population).
Bracketing the issue of Borges et al using an annual U.S. pregnancy but global live birth rate — the choice of pregnancies or births should be consistent — the first estimation approach here suggests 130,000 PPBC cases worldwide annually, without a denominator. The second suggests 13,000 PPBC cases out of 4.5 million U.S. pregnancies (13/4500 = .00288, or .29%), or 364,200 cases out of 130,000,000 live births, for an incidence of .00280, or .28%.
It seems Borges et al also made a decimal mistake here in calling this .0028%. The division in both cases yields around .0028, and .0028 converts to .28%.
This is a substantial over-estimate due to the deflated denominator. What’s a better calculation? Averaging the U.S. PPBC consensus count of around 12,000 or 13,000 U.S. PPBC cases per year yields the numerator 12,500. The denominator takes a little more work.
Revised PPBC incidence estimate
An ideal denominator here would be a U.S. Census estimate of biological mothers who had children in the last 25 years or so — the most at-risk population for PPBC. This doesn’t appear to exist. An available second-best is an estimate of U.S. households with minor children, excluding those headed by single fathers — a plausible correction for mothers who may be missing because they’re dead, and so don’t count in the denominator. Add married couples and single mother households from the 2010 count, since the available annual numbers don’t vary much, and Goddard et al 2019’s references 33-35 for their 12,000 poor-prognosis PPBC U.S. annual diagnosis figure are referring to 1975-2013, 2015, and data from an article published in 2009, respectively. Those figures are 42% married couples plus 57% single mothers heading households with minor kids, of around 66 million U.S. parents in 2010: .42*66 = 27.72 million, plus .57*66=37.62 million, sums to 65.34 million mothers.
Cross-checking that: Approximately 3.5 million births annual U.S. births * 18 years = 63. That’s close to 65.34 million, so this denominator estimate for mothers of children under 18 looks plausible. It even suggests an easy way to increase the denominator to include all women at risk for PPBC, a risk that seems to extend for around 26 years: 3.5*26 = 91 million — though it might make sense to increase the accuracy of the births estimate over the last 26 years based on data, given that the U.S. annual birth rate probably changed more over more time. But not doing that (denominator deflation) may balance out other sources of denominator bias. For instance, there are an unknown proportion of non-biological mothers counted in the household denominator estimate. This probably isn’t a big problem, since single mother households are likely to be headed by biological mothers, and married couples with children under 18 are likely to either contain biological mothers — or to imply the existence of biological mothers outside the household. This doesn’t account for cases where siblings who share a mother might live with different parents, effectively double-counting mothers in such cases. But maybe capping the household proxy estimate for the mother estimate at 18 balances it out.
By this logic, the corrected postpartum breast cancer incidence is around 12,500/65 million, or .000192307692308 (.0192%, or around 1.9/10,000). This appears to be an order of magnitude smaller than currently published estimates. However, the apparent similarity of current estimates to one another is complicated by unit differences.
TABLE 2: Collected PPBC Incidence Estimates
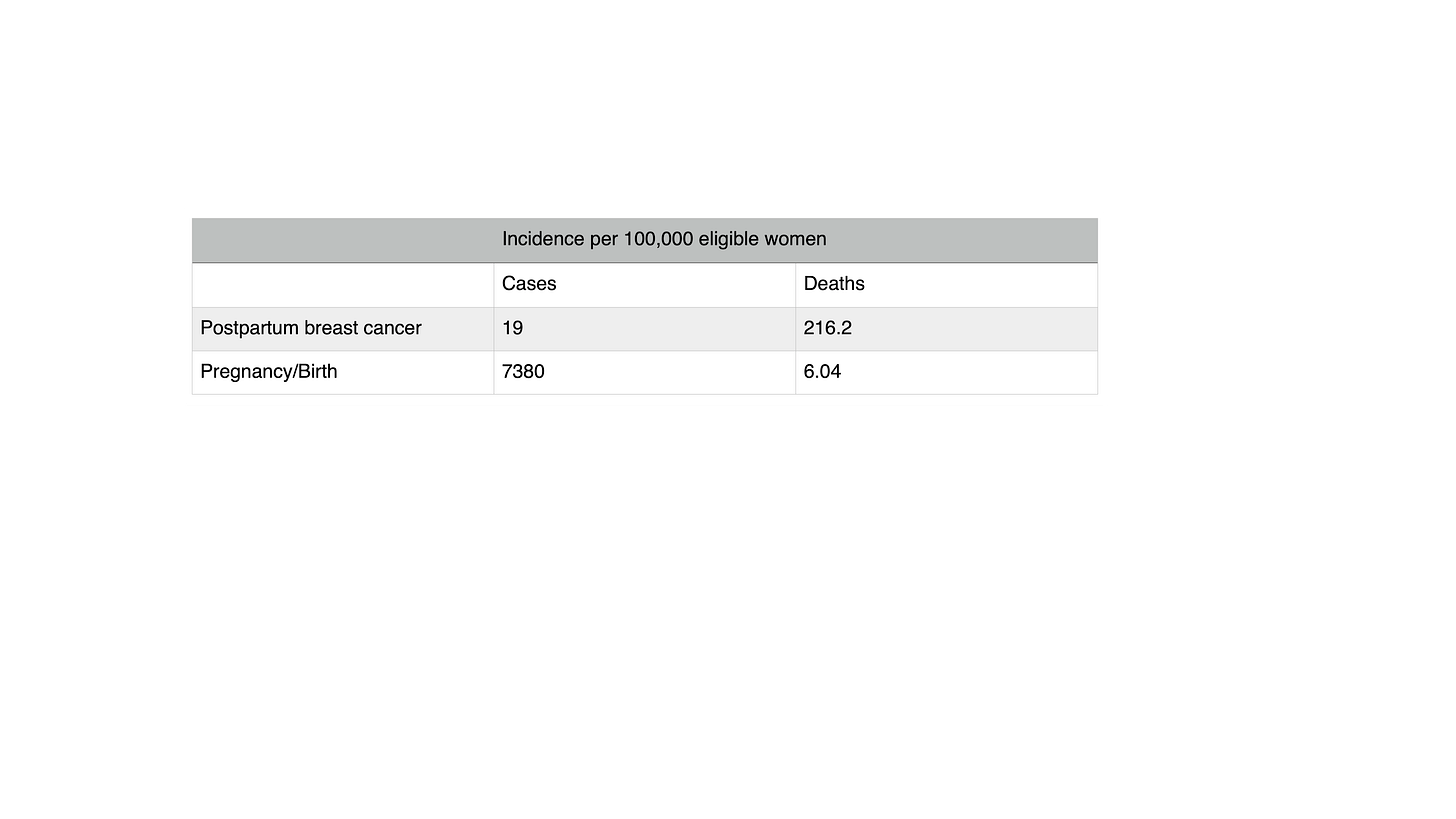
Correcting this incidence matters for understanding hormonal contraception risks, because it suggests PPBC may be highly lethal compared to other breast cancers — but not compared to pregnancy/birth. We still need more information to say. The incidence of PPBC is 1.9/10,000 (or 19/100,000). That’s the same order of magnitude as the incidence of women’s deaths from pregnancy/birth in the UK as reported by the UK Office for National Statistics, 10.9/100,000. But this compares apples (cases) and oranges (deaths). Better compare PPBC with pregnancy/birth — cases with cases — and deaths with deaths. So how common are pregnancy/birth and associated death?
Pregnancy/birth base rate calculation and comparison
The UK Office for National Statistics (ONS) suggests the number of pregnancies is a better denominator than live births for maternal mortality, because pregnancy itself is risky. So calculating the base rate of pregnancy is probably better than calculating the base rate of birth.
According to Guttmacher, the U.S. pregnancy rate hit an all-time low in 2017, with 87 pregnancies per 1,000 reproductive-aged women (i.e., girls and women aged 15-44 years). That’s 8700 pregnancies per 100,000 reproductive-aged women. According to the ONS, the UK pregnancy rate is similar: “The conception rate for women of all ages in England and Wales saw a small decrease from 73.8 per 1,000 women in 2019 to 73.4 per 1,000 women in 2020.” That’s 7380 pregnancies per 100,000 reproductive-aged women, or .0738 — around 7%.
Cross-checking that: The U.S. CDC pregnancy per year estimate was 6,369,000 for 2009, close enough to the comparison PPBC count vintage. That’s the numerator. The denominator is U.S. reproductive-aged women. According to the U.S. maternal and infant health nonprofit March of Dimes, “the population of women ages 15-44 was 64,543,832” in the U.S. in 2020. So the U.S. base rate of pregnancy among reproductive-aged women is around 6,369,000/64,543,832, or .09867712 — around 9.9%.
This means the UK and U.S. annual base rates of pregnancy among reproductive-aged women are in the high single digits. That’s around three orders of magnitude larger than the base rate of PPBC, 1.9/10,000 or .019% annually. This gives us reason to suspect the mortality risk of birth control failure at least partly counterbalances the mortality risk of increased breast cancer. That should have already been the prior, since most reproductive-age women can get pregnant, but don’t get breast cancer.
This compares cases with cases. What about deaths?
Maternal mortality base rate
The U.S. is a notorious maternal mortality outlier among wealthier, more developed countries. In 2021, 1,205 U.S. women died “of maternal causes,” for a maternal mortality rate of 32.9 deaths per 100,000 live births, according to the CDC. In the UK, the comparable rate was just 6.04 per 100,000 for 2018-2020, an order of magnitude lower. It makes sense to use the UK maternal mortality rate here, since there’s a big difference, and the point is to constructively critique Fitzpatrick et al’s UK analysis.
How many PPBC cases and deaths are we talking about in comparison with these pregnancy cases and pregnancy/birth deaths?
PPBC case and death rates by age - opposing trends
The U.S. leads in PPBC research, which is a smaller-numbers game due to its rarity. So using U.S. PPBC case and death data makes sense, the U.S. having a population of around 332 million to the UK’s 67 million. But this assumes the U.S. is not an outlier here. Specifically, it sets up an apples (UK pregnancy/birth deaths) and oranges (U.S. PPBC deaths) comparison, which assumes there’s some reason the U.S. is an outlier in maternal mortality (e.g., inequality) that doesn’t also make it an outlier in PPBC. This could be wrong, e.g., if inequality raises inflammation, which mediates cancer cells seeding lymphatic tissue during involution, causing later PPBC metastasis and death; or if poorer environmental regulation leading to pollution exposure contributes to both.
In the previous post, I mentioned that Callihan et al 2013’s retrospective cohort study of 619 women aged ≤45 years diagnosed with breast cancer during 1981-2011 (the Colorado Young Women’s Breast Cancer Cohort) found cases diagnosed <5 years postpartum had substantially increased risk of distant recurrence (31.1 versus 14.8 percent) compared to nulliparous cases, and even more substantially decreased chance of five-year overall survival probability (65.8 percent versus 98 percent). And that Goddard et al 2019’s replication and extension of these findings with the same Colorado cohort, diagnosed 1981-2014, showed that PPBC diagnosed within 10 years of birth was also associated with increased lymphovascular invasion, lymph node involvement, and metastasis risk compared to nulliparous cases. These analyses seem to form the basis of Virginia Borges’s telling Oncology Times:
A woman who is diagnosed with breast cancer within five years of her last childbirth has a metastatic-free survival rate of only 66 percent at 10 years, compared with a woman who has not had a child at the time of her breast cancer diagnosis, whose metastasis-free survival rate is 86 percent at 10 years.
And women who are more than 10 years out from their last childbirth (not first childbirth) at the time of their breast cancer diagnosis have a survival rate of 78 percent at 10 years, still a statistically significant difference from 86 percent at 10 years.
(Borges was last author on both Callihan et al 2013 and Goddard et al 2019.)
Notice how these two implied mortality rate estimates trend — 34% for PPBC diagnosed within five years of last birth, and 22% for up to 10 years between birth and diagnosis. The younger the woman and the closer to birth a mother is at the time of her breast cancer diagnosis, the worse her survival odds. Yet, the older the woman at first birth and in general, the higher the breast cancer risk…
This highlights an apparent paradox: PPBC can’t be highly lethal across the board, more common in older mothers — and yet more lethal in younger and more recent mothers. Not unless the definition of “highly lethal” is so flexible as to lose some of its meaning. This goes back to the Scylla and Charybdis opposing base rates phenomenon that I raised at the start, illustrating why subgroup comparisons are harder than they seem.
One thing that might explain this paradox is if there are different PPBC subtypes reflecting the same trends as breast cancer writ large: Postmenopausal breast cancers are more common but generally less aggressive than premenopausal ones. Similarly, older age at PPBC diagnosis seems to be more common but predict better survival. Mechanistically, maybe something that selects for cancer survival (e.g., immune suppression from high progesterone in pregnancy) also selects for aggression (e.g., lymphatic tissue seeding). The stronger the selection has to be to overcome a threshold health effect (i.e., in younger mothers who are less likely to develop cancer), the more aggressive the resulting cancer. We have reason to suspect the selection mechanism is related to pregnancy: Breast cancer risk spikes after birth and decreases with time for decades, and mortality risk from breast cancer is also worse closer to birth and decreases with time after.
Overall, this suggests it may be suboptimal to look at breast cancer risk by age category, if what we really care about is death risk. That may skew the death risk calculus in exactly the wrong direction, since older women carry higher cancer risks — but younger women who are diagnosed, have worse prognoses. It may be useful to think of this problem in terms of two subgroup effects that vary by age: (1) the base rate of breast cancer increases with age, while (2) the base rate of death given breast cancer seems to decrease with it. In other words, the Scylla of more diagnosed breast cancer cases threatens older mothers, while the Charybdis of more fatal diagnoses threatens younger mothers.
Maybe bracketing age balances these opposing cancer case and death rate trends. Maybe not. It’s clear they run in opposing directions, but not how the effect magnitudes net out. Is there a general technical term for this sort of phenomenon of opposing base rate trends by subcategory, or another concept it keys into? There’s always causality, which in this case goes back to metastases driving cancer deaths, lymphatic tissue seeding during involution potentially driving postpartum breast cancer metastases, and some unknown factor selecting for more aggressive cancers possibly in that window when younger mothers, who are much less likely to develop breast cancer, do. Maybe the higher the homeostatic threshold the cancer must overcome to seed, the deadlier it is.
PPBC death count and rate
Bracketing possible age subgroup effects ever more gladly, let’s assume 12,500 U.S. PPBC cases diagnosed annually reflect poor prognosis, with something like an average of these mortality rates: (34+22)/2= 28% — an overestimate, as some PPBC cases are diagnosed 10+ years after birth, and PPBC mortality decreases as time between birth and diagnosis increases. That would give PPBC an approximate death count of 3500. But these deaths aren’t annual; two out of three women diagnosed with metastatic breast cancer die within five years. So say 2/3 of 28% of a 12,500 annually diagnosed U.S. PPBC cohort = 2,333.333 deaths in five years. Dividing by five yields 466.6667, or around 467 U.S. PPBC deaths a year.
But the denominator for base rate of PPBC death is cumulative PPBC cases, not annually diagnosed cases or reproductive-aged women. This means around 12,500 * 18 years for consistency of the estimates = 225,000 U.S. mothers diagnosed with PPBC over a minor child’s lifetime. Correcting for deaths: (2,333.333/5) = x/18, x = 8399.999… —> 225,000-8400 = 216,600. So the approximate annual rate of death from diagnosed PPBC is 467 deaths /216,600 cumulative diagnosed cases minus cumulative deaths. That comes to 21.56/10,000, .002156, or .2156%.
How does this compare with maternal mortality?
Incidence of pregnancy/birth and PPBC in terms of cases and deaths
The U.S. annual PPBC death estimate of 467 is fewer than half the U.S. 2021 deaths from maternal mortality, 1,205. The base rate of death in a particular year from PPBC once it’s been diagnosed (21.56/10,000) seems to be an order of magnitude larger than the base rate of death from birth (3.2/10,000). So PPBC is at least an order of magnitude deadlier than pregnancy/birth. But we also need to remember how much rarer PPBC is than pregnancy.
Table 3 shows the incidences of postpartum breast cancer and death from it, and pregnancy/birth and death from it, applied to a hypothetical population of 100,000. This is still something of an apples to oranges comparison that could probably be done better. Maybe it’s bad that the incidence per 100,000 eligible women involves different denominators, but that shows what I need to see: How common are these outcomes once you’ve rolled the dice into the relevant cell to begin with? This tells you how worried to be once you’re in the relevant cell. This means the incidence of PPBC is calculated among mothers with minor children, the previously estimated denominator. The incidence of pregnancy is calculated among reproductive-aged women, and maternal mortality among pregnancies.
TABLE 3: Pregnancy and PPBC Incidence and Mortality
This shows PPBC is two orders of magnitude rarer than pregnancy/birth. A reproductive-aged women is far more likely to get pregnant than a mother is to be diagnosed with PPBC — though many women try to get pregnant, and no one (presumably) tries to get cancer. Then, once a mother is diagnosed with PPBC, her annual chance of dying from it is around 467 annual deaths/216,000 cumulatively (over 18 years) diagnosed cases (assuming new cases roughly replace deaths), which is .002162, or around .216%. This seems suspiciously small given Borges’s claimed 34% mortality rate for PPBC diagnosed within five years of last birth and 22% for PPBC diagnosed up to 10 years postpartum. Sometimes absolute versus relative risks look this different, but these are both absolute risks; so maybe somebody made a mistake.
In any event, converting that risk to x/100,000 yields around 216.2. This means PPBC is two orders of magnitude deadlier than pregnancy/birth.
Overall, PPBC is two orders of magnitude rarer but deadlier than pregnancy/birth. Yet, this doesn’t mean PPBC is necessarily “deadlier” than pregnancy/birth. In absolute terms, pregnancy/birth is about an order of magnitude riskier than PPBC. The deaths per 100,000 tell that story: These rates mean about 6 pregnancy/birth deaths per 100,000 pregnancies annually, versus about 467 deaths per 65.34 million mothers of minor children = x/100,000 —> x = .71472. This is only one order of magnitude difference, but it suggests pregnancy/birth is riskier than PPBC in these terms.
Adding up maternal birth and breast cancer deaths
Getting back to estimating deaths from different contraceptive options, this analysis accounts for mortality from pregnancy/birth plus PPBC. There are other causes of death that may be causally related to things like birth control failure and hormonal contraception use, like domestic abuse and [sic] other cancers. This analysis ignores them.
Accounting for maternal mortality: The UK maternal mortality estimate of 10.9/100,000, or 1.09/10,000, figures into both deaths cells. For withdrawal: 1.09/10,000 = x/2219 —> .241871 deaths from pregnancy/birth associated with withdrawal failure. Given this order, it makes sense to rescale this table to 100,000 and round up to whole integers at the last step. That yields 2.41871 deaths per 100,000 from pregnancy/bith associated with withdrawal failure for now. For the pill: 1.09/10,000=x/986 —> .107474 deaths from pregnancy/birth associated with pill failure, rescaled to 1.07474/100,000.
Adding breast cancer death risks: There are three types of breast cancer death risks that come up in this context. The first is PPBC risk spike after previous birth(s). The second is PPBC risk spike after another birth after birth control failure. And the third is increased breast cancer risk associated with hormonal contraception. Bracket the second type, because it’s unclear what possible multiparity effects are. That means we want to add the first type of breast cancer risk (postpartum spike) to both death cells, and the third (hormonal contraception exposure) only to the pill death cell.
To disaggregate these effects to see the effect of hormonal contraception, ideally we want data on postpartum breast cancer and death risks for women exposed and not exposed. To simplify using what we have for now, let’s use the previously calculated PPBC death risk for both cells, and then add Fitzpatrick et al’s hormonal breast cancer case increase to the postpartum breast cancer context to recalculate an additional death risk for the pill. This overestimates the total breast cancer risk, because the initial PPBC risk spike estimate already includes cases with and without hormonal birth control exposure. Probably double-counting these cases doesn’t matter, because this is a small numbers game and there’s no strong hormonal contraception-PPBC finding in the literature; this should still be done better by someone with PPBC database access to avoid double-counting.
The first type of calculable breast cancer death risk, the PPBC risk spike affecting both cells, was .71472, as calculated in the previous subsection. Now we can total the typical-use withdrawal death cell: 2.41871 + .71472 = 3.133. That rounds to 3.
For the second type, breast cancer death risk from hormonal contraception, we need to combine the case increase from Fitzpatrick et al with the death risk 467/65.34 million. But we’re only looking for the postpartum case increase here, to calculate the death risk for the most at-risk subgroup. Fitzpatrick et al indicate that of their sample’s breast cancer cases (9,498), 897 (9.4%) were diagnosed <5 years from birth, 713 (7.5%) 5-10 years from birth, and 83% with no birth recorded in the last 10 years. This means the majority of diagnosed breast cancer cases in their sample were not at heightened risk for metastasis and thus death, because they weren’t postpartum cases.
This raises a question I can’t answer: If birth spikes premenopausal women’s breast cancer risk, and most women become mothers, then why aren’t most of these cases postpartum? There’s a big discrepancy between this characteristic of Fitzpatrick et al’s data — only 17% of breast cancer cases in their sample being postpartum — and Borges et al’s description of around 50% of premenopausal breast cancer cases being diagnosed within 10 years postpartum.
Another characteristic of Fitzpatrick et al’s data worth noting is that more postpartum cases will still be diagnosed 10+ years from birth that are not captured in this sample. Those will tend to be less lethal cases.
Fitzpatrick et al find that oral contraceptives increase the 15-year absolute excess risk of breast cancer by about 8 cases in 100,000 women aged 16-20, to 265 cases in 100,000 women aged 35-39. So let’s say that the pill adds around (8+265)/2 = around 136.5 breast cancer cases, not accounting for the age distribution in the population. But only around 100-83 = 17% of those cases were postpartum, or around 23.205 cases. How many annual deaths does this spell?
Say those extra postpartum breast cancers were diagnosed: <5 years from birth 9.4% of the time, and 5-10 years 7.5% of the time, the proportion in which they were so diagnosed in this sample. That’s close enough to 50-50 to warrant averaging the previously discussed 34% mortality for PPBC diagnosed within 5 years of last birth and 22% for up to 10 years, for 28% mortality. Recall 2/3 women diagnosed with metastatic breast cancer then die within five years, so 23.205 cases *.28 mortality rate/5 years = 1.29948, or around 1 death. Add that to 1.07474 (deaths from births following pill failure) and .71472 (deaths from PPBC as if without hormonal birth control exposure), and it looks like the estimated deaths in the typical-use pill cell are 3.08894. This also rounds to 3.
Absolute, relative, and net death risks
The absolute risk of death from pregnancy/birth and breast cancer is 3/100,000= .00003 (.003%) for both the pill and withdrawal under typical efficacy rates. The relative risk of death is no different between these options. The net death risk is zero.
There are still differences here — qualitative differences in how women live or die. Some of these differences are in the number of children they have. Some are from pill side effects, which are common and potentially crippling. An unlucky few are from very different types of deaths — relatively sudden deaths from pregnancy/birth, versus long and painful deaths from metastatic breast cancer. Given the large role of chance in these rare outcomes, it seems cruel and illogical to call taking these risks anything like choice or consent. Do we really lack better language?
tl;dr
Informed consent is a great idea. We should create it.
Don’t Say:
Hormonal contraception increases breast cancer risk a little, but prevents conception a lot. Pregnancy is so much more common than breast cancer that this results in net zero deaths. So “just get on the pill.”
Do Say:
“Show me the bodies.”
Normal statistical analyses present risk by stratifying on covariates. In this example, Fitzpatrick et al’s analysis stratified on whether a woman had given birth. That approach disappears crucially important subgroup information into aggregate effect estimates that apply to exactly no one.
Researchers can improve science and society by doing some extra thinking to give at-risk groups more directly relevant insight into when they might want to duck. As an added bonus, then everyone gets better information on which to base their own life decisions. The numbers don’t dictate a right answer for anyone. Quality of life, quality of death, and autonomy all matter. But information on life or death risks should be the foundation of informed consent.
That said, apparently simple things like subgroup risk assessment, denominators, and decimal conversions can be tricky. Correcting mistakes in the medical literature here tipped the net death balance from a small survival advantage accruing to women using withdrawal over hormonal contraception to net zero. That advantage was in terms of gruesome metabolic breast cancer deaths.
It would be great if a free online calculator did this type of comparison for people making everyday medical decisions. But making a good one might be impossible, because it takes a lot of actual reading and thinking to do this right. So it would probably take a highly collaborative format to give it a try.